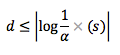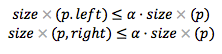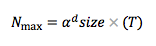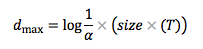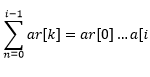Binärbaum
In diesem Beitrag wird es um binäre Suchbäume gehen. Aus diesem Grund erkläre ich zunächst, was denn überhaupt ein Binärbaum ist.
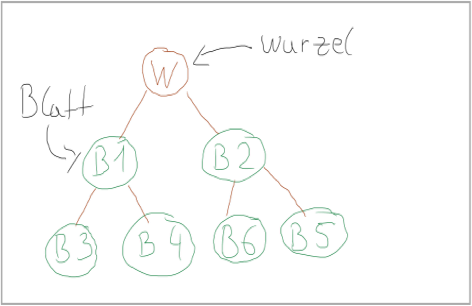
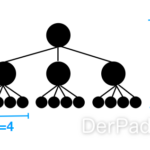
Ein Binärbaum ist ein Spezialfall von einer Baum-Datenstruktur. Jeder Knoten hat maximal Zwei Kind-Knoten, einen Linken und einen Rechten. Ein vollständiger Binärbaum hat 2^d Blätter und 2^(d + 1) – 1 Knoten.
Binäre Suchbäume
Ein binärer Suchbaum eignet sich hervorragend für eine binäre Suche. Für jeden Knoten n gilt:
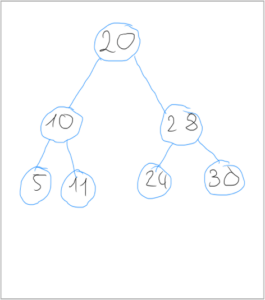
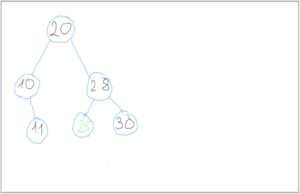
Beispiel für die Suche nach einer Zahl in einem binären Suchbaum
Wir suchen die Zahl 24 in dem Beispielsbild oben und gehen wie folgt vor:
24>20⇒right 24≤28⇒left 24=24⇒found
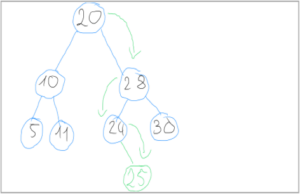
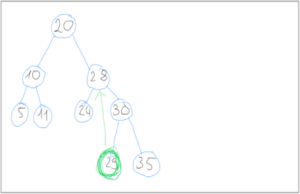
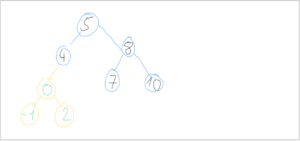
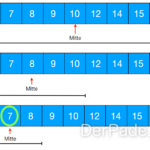
Beispiel für das Einfügen einer Zahl in einen binären Suchbaum
Um die Zahl 25 in den binären Suchbaum einzufügen, müssen wir wie folgt vorgehen.
Löschen einer Zahl aus einem binären Suchbaum
Hier muss eine Unterscheidung nach der Anzahl von Kind-Knoten erfolgen. Je nach dem ob der zu löschende Knoten noch Kind-Knoten besitzt, können wir diesen nämlich nicht so einfach aus dem Suchbaum löschen.
- Besitzt er keine weiterem Kind-Knoten, können wir ihn einfach löschen
- Besitzt er einen weiteren Kind-Knoten, ersetzen wir den zu löschenden Knoten mit seinem Kind-Knoten
- Besitzt er zwei Kind-Knoten, ersetzen wir den zu löschenden Knoten mit dem Minimum des rechten Pfades und entferne diesen Minimum Knoten.
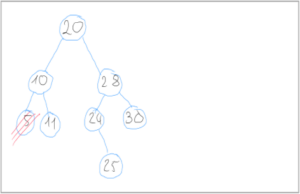
1) Löschen ohne Kind-Knoten
2) Löschen mit einem Kind-Knoten
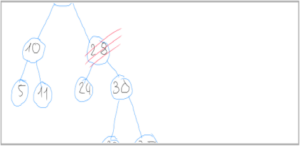
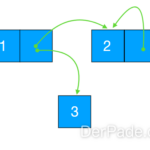
3) Löschen mit zwei Kind-Knoten
Balancierter binärer Suchbaum
Da im worst-case die Effizienz von binären Suchbäumen für das Entfernen und Hinzufügen von Knoten auf 0(n) sinkt, verwendet man in der Praxis balancierte binäre Suchbäume.
Ein balancierter binärer Suchbaum erfüllt folgende Eigenschaften:
- es gibt n Knoten
- die maximale Tiefe ist d
- d <= c * log n
Dies garantiert, dass binäre Suchbäume in 0(log n) bleiben.
Rebalancing eines binären Suchbaums
Um einen binären Suchbaum neu zu Rebalancing, muss man wie folgt vorgehen:
- Erzeuge eine sortierte Liste.
- Erzeuge aus der sortierten Liste einen balancierten binären Suchbaum
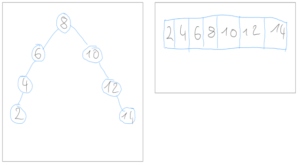
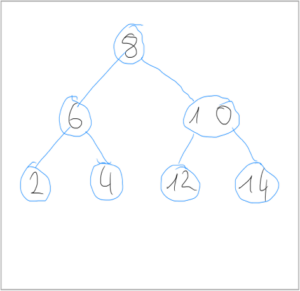
Gesamte Laufzeit:
O(n + n) = O(n)
Scapegoat-Tree
Ein Scapegoat-Tree ist ein selbst-balancierender binärer Suchbaum, der bei jedem Einfügen und Entfernen von Elementen den Baum auf, “Balanciertheit” prüft und ggf. den unbalancierten Knoten sucht und ein Rebalancing durchführt.
Sortiertes Einfügen im Scapegoat-Tree
Dieser Vorgang funktioniert im Allgemeinen wie bei einem binärem Suchbaum. Jedoch wird die Tiefe des eingefügten Knotens zwischengespeichert. Danach wird auf “Höhen-Balanciertheit” getestet:
- d ⇒ Zwischengespeicherte Tiefe
- s ⇒ Size, größe des Trees.
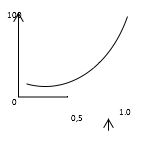
- alpha ⇒ wert Zwischen 0.5 Und 1.0, wobei 0.5 für einen perfekt balancierter Baum steht und 1.0 für einen schlecht balancierten Baum steht.
Falls der Baum nicht alpha-Höhen-balanciert ist, muss der „Sündenbock” gefunden werden. Dabei wird an der zwischengespeicherten Höhe d begonnen und der erste Eltern knoten p gesucht, der nicht alpha-balanciert ist und für den gilt:
Danach wird der Knoten rebalanciert.
Zusammenhang von Gewichts-und Höhenbalanciertheit
Wenn ein Baum nicht a-höhen-balanciert ist, existiert mindestens ein Knoten im Baum, der nicht a- gewichts-balanciert ist.
Um diese Behauptung zu begründen, betrachten wir zunächst die maximale Tiefe des Baums. Die maximale Knotenanzahl auf der tiefsten Ebene dieses Baums ist:
Die tiefste Ebene sollte die Ebene sein, auf der N_max = 1 ist. Für die tiefste Ebene gilt:
Beispiel Einfügen einer Zahl
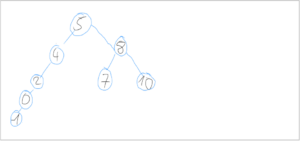
Für „-1″:
- a × size = 0,6
- left size <= 0,6 ✓
- right size <= 0,6 ✓
- left und right size sind 0
Für „0″
- a × size = 1,2
- left size <= 1,2 ✓
- right size <= 1,2 ✓
- left size = 1
- right size = 0
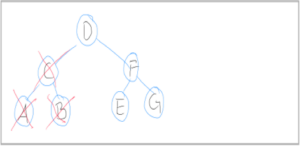
Für „2″:
- a × size = 1,8
- left size <= 1,8 X
- right size <= 1,8 ✓
- left size =3
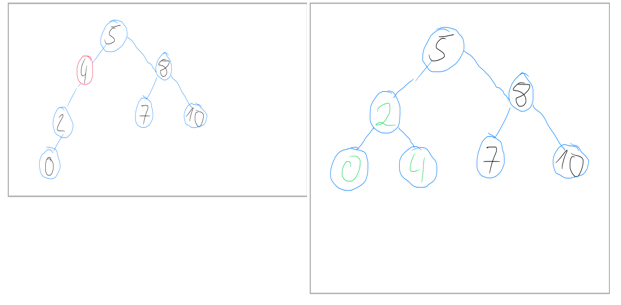
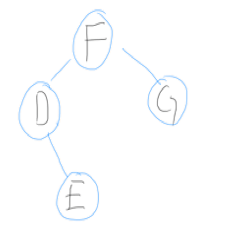
- wir haben die „2″ als Sündenbock identifiziert. Demnach muss an dieser Stelle ein Rebalacing stattfinden und wir erhalten den folgenden Baum:
Beispiel für das Löschen einer Zahl
Wenn einseitig gelöscht wird, kann die Balanciertheit darunter leiden. Wenn das Folgende gilt, muss der ganze Baum neu balanciert werden:
size<α·maxsize
Dies ist ein perfekt balancierter Baum für den gilt:
Wir löschen nur solange Elemente einseitig aus dem Baum, bis ein Rebalancing nötig ist.
Es gilt:
size<α·maxsize 4<4,2
Und daraus folgt unser neuer Baum:
Laufzeit von Scapegoat Trees:
- b-search: O(log n)
- Sorted Insert: O(log n)
- Sorted Remove: O(log n)
Scapegoat Tree im Vergleich zu Red-Black-Tree und AVL-Tree
Red-Black-Trees (Binärer Bäume) eignen sich für häufiges Einfügen und Löschen besser, während man bei Scapegoat Trees Alpha frei wählen kann.
Array als Binärbaum
Es ist möglich einen Binärbaum mittels Arrays zu implementieren. Im Vergleich zu einer verketteten Liste als Datenstruktur ergeben sich folgende Vorteile:
- Referenzen werden errechnet
- Die Daten liegen im Speicher direkt hintereinander, wodurch sich ein schnellerer Zugriff ergibt
Heap
Heaps sind mit Arrays realisierte Bäume, die eine Heap-Eigenschaft besitzen. Die Kind-Knoten haben dabei immer einen größeren Wert, als ihre Eltern-Knoten. Für weitere Informationen siehe hier.
Trie – Präfixbaum
Ein Trie, oder auch Präfixbaum genannt, gehört zur Familie der Suchbäume. Anders als bei einem binären Suchbaum kann ein Eltern-Knoten in einem Trie mehrere Kind-Knoten haben. Er repräsentiert nicht den Wert selbst, sondern nur den Präfix.
Beispiel für die Suche in einem Trie
Ein Trie, der aus den Worten „bier”, „bla” , „car”und „biene” besteht .

Weitere Beiträge aus dieser Serie
- Binäre Suchbäume in der Informatik einfach erklärt
- Durchsuchen von Array-Listen - Lineare und Binäre Suche
- Sequentielle Datentypen
- Algorithmische Techniken - Brute Force, Greedy, Teile und Herrsche, Dynamische Programmierung und Backtracking
- Lazy Evaluation und Streams
- Die Liste als abstrakter Datentyp
- Korrektheitsbeweise von Klassen und Schleifen
- Der Graph als abstrakter Datentyp