Korrektheitsbeweise

Um einen Programm-Code auf Korrektheit zu prüfen, gibt es die sogenannten Korrektheitsbeweise. Diese unterteilen sich in Schleifeninvarianten und in Klasseninvarianten.

Schleifeninvariante

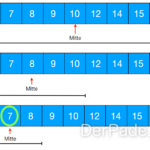
Eine Schleifeninvarianten beweist man häufig mit der Methode der vollständigen Induktion. Dabei schaut man sich ein bekanntes Element, beispielsweise mit dem Index 0 oder 1 an und prüft, ob-die Aussage gilt. Danach prüft man ein Element i + 1.

Beispiel:

<?php

$sum = 0;
for ($i=0; $i<10; $i++) $sum+=$i;

?>

1. Aufstellen der Schleifeninvariante(n) 
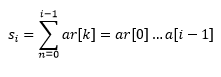
2. Gelten diese Schleifeninvarianten für i = 0? ⇒ Ja, denn die Summe vom nullten Element ist sowohl im Code als auch in der Schleifeninvariante gleich.
3. Gilt diese Schleifeninvarianten auch für I + 1? ⇒ Ja, denn es gilt:

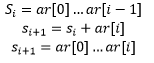
Klasseninvarianten

Bei einer Klasseninvariante kann man eine Aussage über die strukturelle Garantie einer Klasse treffen.

5 Schritte zum Beweis von Klasseninvarianten:

1. Beweis nach jedem Konstruktoraufruf.
2. Variablen bestimmen, die für diese Klasseninvariante eine Rolle spielen.
3. Bestimme die Methoden, die keine Variablen aus ändern.
4. Beweise oder treffe eine Aussage darüber, weshalb die Methoden aus 3. keine Rolle für die Invariante spielen.
5. Beweise die Methoden, die eine Änderung an den Variablen aus 2. durchführen.

Beim Beweis in Punkt 5 kann man davon ausgehen, dass vor jedem Methodenaufruf  die Klasseninvariante gegolten hat. Wenn die Methode nur einfache Anweisungen enthält, kann man sie direkt als Gleichung aufstellen und so umformen, dass wieder die Aussage der Klasseninvariante herauskommt. Wenn die Methode eine Schleife enthält, oder rekursiv definiert ist, muss man sie mit der vollständigen Induktion beweisen.

Weitere Beiträge aus dieser Serie

• Binäre Suchbäume in der Informatik einfach erklärt
• Durchsuchen von Array-Listen - Lineare und Binäre Suche
• Sequentielle Datentypen
• Algorithmische Techniken - Brute Force, Greedy, Teile und Herrsche, Dynamische Programmierung und Backtracking
• Lazy Evaluation und Streams
• Die Liste als abstrakter Datentyp
• Korrektheitsbeweise von Klassen und Schleifen
• Der Graph als abstrakter Datentyp